Fully Homomorphic Encryption (FHE) has emerged as a powerful tool, allowing computations on encrypted data without decryption. However, existing FHE systems struggle with large integers, a critical requirement for many real-world applications. This blog post explores a new groundbreaking FHE system by Boneh and Kim. They designed a system to handle large integers efficiently, offering significant performance improvements over traditional methods.

The Challenge of Large Integers in FHE
Fully Homomorphic Encryption (FHE) enables secure computations on encrypted data, but most existing systems are optimized for small prime numbers. Therefore it can not deliver on its promises.
In particular, this limitation becomes a bottleneck in applications requiring arithmetic over large integers, such as cryptographic signatures or secure multi-party computations. For example, FHE can in principle make the threshold version of widely used signature schemes like ECDSA and Schnorr much more efficient using a Universal Thresholdizer (source and source). Think one round ECDSA: as efficient as ECDSA, but threshold.
Unfortunately, both Schnorr and ECDSA operate over 256-bit or 384-bit primes. Current FHE systems perform poorly when handling such large moduli, leading to impractical computation times.
In short, FHE holds great promise for secure computation. Yet its inefficiency with large primes prevents it from realizing its full potential in practice.
How the Nested RNS System Works
The new FHE system addresses this challenge leveraging a 6th-century well known result: the Chinese Remainder Theorem (CRT). It lets you find a number from its remainders when divided by coprime numbers. Details follow.
The core innovation of the paper lies in its use of a nested Residue Number System (RNS). This architecture composes three layers of residue systems, enabling efficient modular arithmetic over large integers. The system leverages the CRT to represent large integers as a combination of smaller moduli, which can be processed in parallel within a single ciphertext.

The first layer of the RNS system (the one at the bottom in the figure above) handles small moduli. And the second and third layers extend this to support larger integers. By using homomorphic base conversion (see next paragraph), the system can switch between different moduli without expensive modular reduction operations.
Base conversion works like this. Given number 123, you split the number into smaller parts, like 1, 2, and 3. Now, instead of dealing with 100+20+3, you can work with 1, 2, and 3 separately, which is much simpler. Homomorphic base conversion is like this, but for encrypted numbers.
Such approach allows for efficient arithmetic over large integers, significantly improving performance. See the last section of this post: the system achieves a thousand-fold improvement in multiplication throughput and a tenfold reduction in latency compared to existing implementations like TFHE.
In summary: A multi-layered architecture enables efficient arithmetic over large integers. It breakes them into smaller, parallelizable components, significantly improving performance.
Performance Gains for Real-World Applications
Let’s see the details of how the RNS system compresses days of computation to a handful of hours.
One example proposed by the authors is in homomorphic signing, a process where cryptographic signatures are computed on encrypted data. In this case, the system reduces the time to generate a single ECDSA signature from two days to just a few hours. This improvement is critical for applications like threshold and blind signatures, which require fast and secure computations.
To be clear: the ECDSA signature is done on current NIST-approved parameters This proves that the system also supports a wide range of moduli, from 256-bit primes used in elliptic curve cryptography to 2048-bit RSA moduli.
This flexibility ensures that the system can be applied to various cryptographic protocols without compromising security. The system’s ability to handle multiple slots of smaller moduli in parallel does enhance its efficiency!
The new FHE system offers significant performance gains, enabling practical applications like homomorphic signing and secure multi-party computations.
Practical Implications for Businesses
For businesses that handle sensitive information, the new FHE system opens up new possibilities for secure data processing. Additionally, the RNS system can also help companies already dealing with FHE systems.
For example, financial institutions can use the system to perform secure computations on encrypted transaction data, while healthcare providers can process encrypted patient records without compromising privacy.
Autist Note: this is a different use case from MPC. With FHE the computation is done locally on encrypted data by one party only. MPC deals with multiple parties who make a joint computation without revealing their data.
The system’s ability to handle large integers efficiently also makes it suitable for advanced cryptographic companies. For example, the open-source cryptography company Zama specializes in Fully Homomorphic Encryption (FHE) solutions, particularly for blockchain and AI applications. They developed the famous TFHE-rs, a Rust implementation of the TFHE Scheme. Incidentally, Zama published their first major version of TFHE-rs yesterday.
The work by Boneh and Kim presented in this post makes Zama’s implementation of integer multiplicaton 10X faster (less latency) and 1000X more scalable (higher throughput, multiplications per second), according to the authors of the paper. See image below
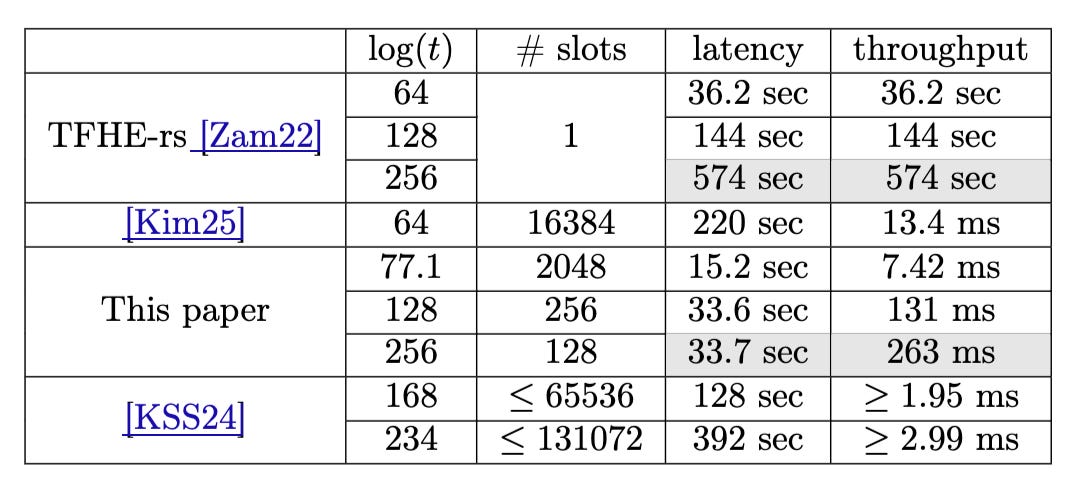
In summary, the new FHE system provides businesses with a powerful tool for secure data processing, enabling new applications for any kind of business, including those dealing with AI and cryptography itself
Conclusion
This latest research represents a significant leap forward in secure data processing. It enables efficient arithmetic over large integers thanks to its nested RNS architecture, addressing a critical limitation of existing FHE methods. It is a step forward to make FHE practical for real-world applications.




