1. Introduction
Multiparty computation, or MPC, what's that? Why people say that this is the answer to key management and privacy problems in general?
The definition of MPC may seem broad at first glance, but it becomes more precise as you go deeper into the subject.
In general MPC is any kind of joint computation between parties. Inherent in the definition is the fact that each party will not share its own input. Yet the computation uses inputs of all parties participating. The first example comes from Andrew Yao (1982). He invented the millionaire problem, where two people want to know who is the richest among them. Together they have to compute the operation “less than” with a twist. They must not reveal their real net worth. At the end of the computation, both parties will know who among them is the richest.
To reiterate. The previous example is MPC. A simple exchange of messages between you and me is not MPC since you can see my input. So no: SSL/TLS and the chat between you and your friends is not MPC, both of them have no joint computation. Still, you may consider some MPC some key distribution protocol between devices.
Note: Some people differentiate between “multiparty computation” and “secure multiparty computation.” (SMPC). By this distinction: a conversation between you and me is MPC; the Millionaire’s Problem is SMPC. With this interpretation, any kind of interaction is multiparty computation. And this renders the term too broad to matter. For this reason, we use both “multiparty computation” in place of "secure multiparty computation".
There are many branches of multiparty computation. We have the secret sharing primitive, used in threshold signatures for example. Everybody dealing with a blockchain knows that. What you may not know are the other branches. Primitives like oblivious transfer and garbled circuits. Or functions such as private set intersection. These are not popular in the blockchain space, but new proposals are coming.

Note: MPC started in the 80s. Still, up until now it wasn't efficient due to cumbersome protocols and weak hardware. We had to rely on specific (instead of general) MPC protocols for specific application. So we could perform secret sharing or some kind of auctions, yet we couldn't have a search engine running as MPC.
The end goal of the series is to explain how each branch of multiparty computation work. In this first part we go from polynomials to threshold signatures.
Of course, we cannot talk about everything related to this topic. In dedicated posts we'll see how specific protocols actually works. For example, in this post, we talk about distributed key generation systems. In one or many other posts we will go into the details of a or more specific distributed key generation system.
2. Polynomial Intro
Polynomials are particular type of mathematical function with a single input. The output is a sum of many multiplication of the input in various degrees and a constant. Below the formal representation of a polynomial of degree T-1.
And here are some polynomials:
A surprisingly simple yet powerful property. Given T points, you can determine one (and only one) polynomial of degree T-1. One way to do it is Lagrange interpolation. We treat it as blackbox: you enter the point, it gives you the polynomial.
What does this mean in practice? Imagine you’re plotting points on a graph. If you have two points, you can draw a single line (degree 1, so T = 2) through them. Add a third point, and you can draw a single parabola (degree 2, so T = 3). This concept is the basis of complex cryptography systems. One is secret sharing schemes, which we explain below
3. Secret Sharing
3.1 Example scenario
Alice has a file. We don't care about the size of this file. A string of 64 alphanumerical characters or a 1GB video of her daughter’s first birthday party are the same. What's important here is that Alice considers this file as sensible and private. Yet she wants to be able to recover this file in the future. Sure, she could back it up in her external hard drive. But storing things in the house can be very prone to losing it if your house burns down. We have been sadly reminded of that. Another idea can be to encrypt the file and upload on Google Drive or dropbox. But then she has to remember the password. Can you see the circularity of this problem? Where do you store the file containing the password (it is a strong password, so it is impossible to remember)? And. She needs to be sure that Google Drive or dropbox will be there in 30 years. If the file contains the secret key for your cryptographically secured coins, you wouldn't bet on it. What do?
Alice can split this file into 3 overlapping parts (called shares). Then she uploads each share in a different cloud storage system (share sh1 in cloud storage CS1, sh2 in CS2 etc.). The share overlap: any couple of shares can re-create the whole file. Hence Alice doesn't need all 3 of them!
More formally, Alice can use a two-algorithms system, called secret sharing. The first algorithm is the sharing algorithm. It takes the file as input, a number N(=3 in the example) of shares, and the number T(=2 in the example). We refer to T as the threshold, as it is the least required to recreate the secret. The second is the reconstruction algorithm. It takes at least T shares and outputs the original file.
This is why it’s called secret sharing. If fewer than T cloud storage systems collude, they cannot reconstruct the secret. In particular, no single node or receiver can determine the file’s content from the single share it holds.
There are various methods to achieve this. The simplest is Shamir’s Secret Sharing protocol, based on polynomials. We present it below
Autist Note: those interested in other non-polynomial based secret sharing mechanism read the survey by Beimel.
Sharing algorithm
The sharing algorithm in Shamir secret sharing is actually very easy. As we said before there are polynomials involved. In polynomials, the constant term, a0, is the only part without a variable.. In Shamir secret sharing, this value is the secret itself. This is possible since your computer stores files as bytes, and so numbers. So given the right representation of the data, you can embed it into a polynomial.
Note also that a0 is the evaluation of the polynomial f in 0. For know just know that, we’ll use it in the reconstructing phase
Let's stay with the simple case of a line, so degree 1=T-1 and therefore T=2. Hence, we can see that if we wanted to represent the file, i.e. a0, on a graph we can actually do that
Remember the line is a polynomial of the degree 1. So Alice creates a polynomial by randomly sampling its second coefficient, a1
Now let's say that Alice has 3 cloud storage services in mind. Let's say that she list them as. CS1, CS2 and CS3. Since she has the polynomial f she can compute the shares sh1, sh2, sh3 by evaluating the polynomial in 1, 2 and 3. Graphically she will get something like that.
Now Alice gives sh1, sh2, sh3 to the respective cloud storage system. The sharing algorithm terminates.
It's easy to see how to generalize that. Your file/secret is always a0. For a threshold T, you sample T-2 other coefficients so that the polynomial f has the desired degree of T-1. If you have N cloud storage systems, you create N evaluations of the polynomial f.
Let's see how any single cloud storage system cannot know what the secret is. Let's say that CS2 wants to know what the secret is. This cloud storage system only has sh2 at its disposal. So, how can it determine the correct values of a0 and a1, given that an infinite number of lines can pass through a single point? (recall: a0 and a1 are the coefficient of the polynomial). Below a graphical representation of the situation CS2 is in.
It's easy to see that any of the a0 can be the right one. In mathematics we say there is equal probability for all a0 to be the right file. With infinite numbers, the probability of any single one being correct is infinitesimal. Which means zero.
Reconstruct
Some time passes. Alice wants to retrieve the original file. What she will do now is very simple. She has to remember at least a couple (T=2) of the cloud storage used. She doesn’t need to know the specific number, like whether it was Google Drive CS1 or CS2. She only needs to know which cloud storage she used.
After that, she will ask to at least two of them for their share. She will be in a situation like that:
As you can see the two shares she received don't have number, because she doesn't know the order of the share used. She doesn't have to remember that, and the cloud storage doesn't know the number Alice assigned to it. But you can see and imagine a line passing through them. The secret is the intersection of this line with the y-axis, meaning the evaluation of f in zero.
More formally, once Alice receives the two points from the cloud storage systems, she can determine the coefficient of the line passing through them. She does this using the Lagrange interpolation blackbox mentioned earlier in this post. After that, she's able to evaluate this polynomial in any point. In particular she's able to evaluate this point in 0 obtaining a0 which is the secret/file.
The protocol terminates and Alice has got her file back.
Intermezzo 1: Some people are good, others are bad
This is a platitude. Yet this will be very important throughout this series on multiparty computation. To make a long story short All good people are alike; each bad person is bad in its own way - semicit.
For this reason, we have to make assumtpions. What do we think about the people we are giving shares to? Are all them good? Will they behave reasonably well up until they can get something out of it? Or are they malicious actors that will do whatever they can to break your file secruity, just for the sake of it?
In cryptography, we distinguish between honest-but-curious (or passive) adversaries and malicious (or active) adversaries. The former seem good on the outside, but on the inside they may try to get more information that what they got. Think CS2 trying to extrapolate (alone) information from sh2 in the example. Shamir secret sharing is secure against any amount of passive adversaries. That's because singularly any party can notextrapolate information beyond the share they received.
The latter, the active adversary, defies rules and tests limits. Meaning. It can send wrong messages or abort in the middle of the protocol etc etc. Whatever you think, the active adversary can do that.
How does Shamir secret sharing do against active adversaries? Well, the protocol is secure up until T-1 active adversaries. In fact, if T active adversaries start to collude, they will reconstruct the secret. Or if they do not provide their share to Alice, she cannot reconstruct the secret! So T-1 is the upper bound of active adversaries tolerated by Shamir secret sharing.
Autist note: These are basic questions. Other questions that we will not go into in this introductory post, are: where they bad from the beginning? Or did they become bad after, or during parts of the protocols? How we operate the little details of the protocols will change based on these are assumptions.
We assume that people are either good or bad from the beginning, people will never change their state. This is not such a strong assumption: you may assume that every person is malicious. We are trading efficiency for security. But dealing with sensible information and privacy, we already gave up a little on efficiency
Intermezzo 2: Digital Signatures
It's 2024 and you probably are here because somehow you deal with the Blockchain either from a speculation standpoint, investment standpoint, or because you are a developer. In any case, you know that the transaction you have to sign the transaction itself. This transaction is signed digitally, meaning that there is a cryptographic protocol that acts on the transaction/ message and produces an output that we will call signature..
Of course, digital signatures are not only used in Blockchain, but in also variety of places, such as software for integrity of updates. If you're interested in that you can easily ask to ChatGPT.
Generally, the signature is done by one party/device only. Even in the case of multi signatures (e.g. in BTC), there is a signature for each device/ participant involved in the signature of the transaction
Note that a digital signature scheme is a collection of three algorithms, namely, key generation, the signing algorithm, and the verification algorithm:
The key generation algorithm takes as input some security parameter, such as the length of the key, and gives in output, the private key and the public key. This is a probabilistic algorithm, you run twice with the same input you get two different outputs.
The signing algorithm takes as input the private key and the message and outputs the signature. This is a probabilistic algorithm, meaning the signature in output will be different if the algorithm is run twice, even if it has the same inputs. Autist note: this is one security requirement needed for the unforgeability property of digital signature scheme
The verification algorithm takes as input to the public key, the signature and the message and just outputs true or false, depending if the verification algorithm is successful or not
Examples of digital signature schemes are: ECDSA, Schnorr and BLS.
4. DKG
If we already have a system to sign transactions, where does MPC fit in? It becomes essential in scenarios involving large financial transactions. You don’t want a single entity to hold 100% of the signing authority. Instead, you want to distribute signing power across many participants. We call this set of participants a group.
In this post, we explore how to distribute signing power equally among all parties. Meaning everyone has the same level of authority, with no hierarchy involved. (
Autist Note: This is a strong assumption. And there are also ways to put in place hierarchical structures for signing if needed.
Distributed digital signature schemes are like a digital signature scheme. But distributed. Instead of a key generation algorithm, we have a distributed key generation algorithm (or DKG). And instead of a signing algorithm, we have a distributed signing algorithm. The verification algorithm is the same since the signature produced by distributed. A signature generated from distributed signing algorithm is indistinguishable from a signature generated by normal signing algorithm.
In this section, we present a DKG and we take the time to analyze each step to see why it's needed
Here's a DKG tl;dr. Let's say that we have three parties (N=3) and we want to have a threshold T=2. The protocol has the following steps (we are using a simplified version of this 2024 paper by Katz, Fig2, p14)
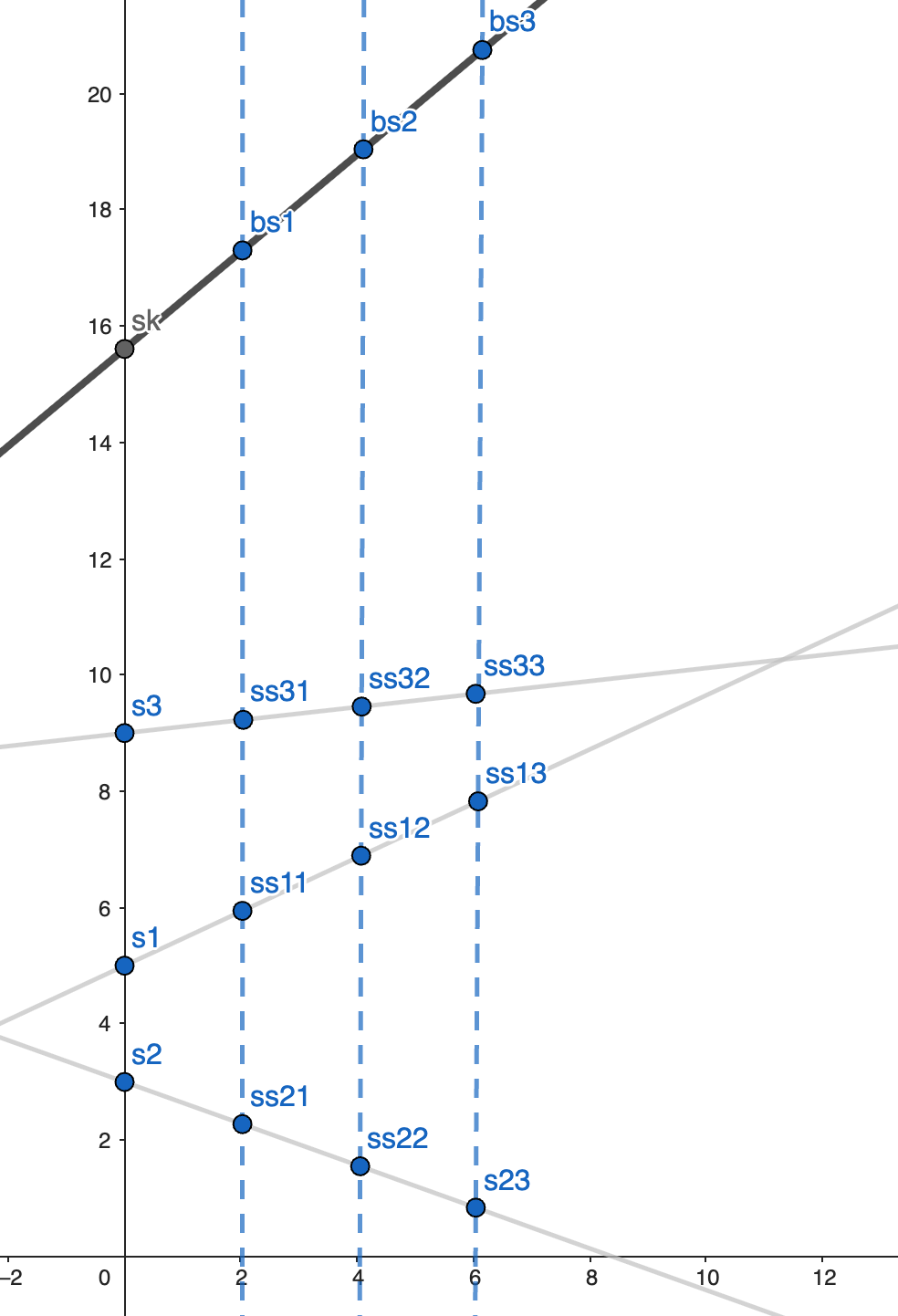
Every participant creates a secret s (party 1 creates s1 etc)
Each participant uses Shamir secret sharing to share his secret to all participant, including himself. Let's call them the “small shares”. So party one creates ss11, ss12, ss13. Meaning: ss11 is the small share for himself, ss12 is the small share that sends to party 2 etc
Each party, after receiving the shares from the other parties and himself, sums these shares into one. Let's call it the big share. Each party has one big share: party1 has bs1, part two has bs2, and party3 has bs3.
Below you can see from a protocol point of view:

A graphical representation of the situation is as in Figure below. The grey lines are the Shamir secret sharing lines, i.e. where all the small shares “stay”. The blue dashed line are the sum lines to create the big shares. Know that those big shares are always aligned , assuming the parties create small shares correctly. The intersection of the line from the big shares with the y-axis is the secret key sk “representing” the group.
Autist note. In general. The big share always lie on a polynomial of the same degree as the degree used for creating the small shares. We can prove it mathematically, and we will show that in a following post.
It is crucial to understand that the secret key is never revealed to any party at any point during the protocol. In theory, the key exists. It's just never computed. Unless we have two rogue parties that collude. This scenario highlights the critical distinction between passive and active adversaries:
If we assume only passive adversaries, then no party will collude, and the secret key stays secret. It's rational. Generating the secret key contradicts the interests of any rational adversary or participant. And t he primary goal of distributed key generation (DKG) is to decentralize control. If some parties collude to reconstruct the secret key, each colluding party owns the key. Hence it gains unilateral signing authority on behalf of the entire group, including their fellow colluders! Such collusion would result in a loss of power for all involved. In fact as each party would give up the protection provided by decentralization. Rationally, collusion doesn't make sense
Remmber. Active adversaries ar those who may attempt to break the protocol solely to disrupt it. They could collude to reconstruct the secret key. This vulnerability highlights the importance of the parameters used in the distributed key generation (DKG) protocol. A DKG protocol tolerates less than T adversaries. If threshold T = 2 then the protocolo tolerates one adversary.
Autist Note: Aside from collusion, active adversaries could send invalid or fake shares, e.g. shares that do not lie on the correct polynomial. To address this, an additional step is required in the DKG protocol. Parties commit to their shares and provide proof that the shares lie on the same polynomial. This results in a verifiable secret sharing (VSS) scheme. It combines secret sharing with cryptographic commitments to ensure correctness. A well-known example of aVSS algorithm is the Feldman one.
5. From DKG to Threshold Signatures
Each party has his big shares. Now the group can proceed to use the key sk as they see fit. For example they may use the key to sign messages. In this case we talk about Threshold Signatures, and we see that in this section.
To create a signature we have two ways. We call combine and sign the former and sign and combine the latter.
The combine and sign method makes all people combine their shares into one secret key, and then use that to sign. In sign and combine, each node/party signs a message with its share and sends it to the other parties. it is not a valid signature, it is a partial signature. All parties then combine their partial signatures into the whole signature. Both methods end with a valid signature. What to chose?
Only the second makes sense. To see that note that in the combine and sign method, the parties will know the total secret key. This the same thing happening with the active attackers as before. We would have any party have 100% of the power to sign on behalf of of the group.
So the only way to create a signature in a threshold environment is by making each party to create a partial signature and then combine the partial signatures into one complete signature.
In this case, there are two operation. The first is computing the partial signature. The second one is combining all the partial signatures. Producing the partial signature is easy, since this is a normal signing operation. You see the share of each node as a private key. Also. This partial signature is indistinguishable from real signature.
The tricky part is the combine part. Meaning the combination algorithm of many signatures into one complete signature. Here is why we distinguis between a threshold friendly or non-threshold friendly digital signature scheme. Is it easy to combine partial sigantures? Yes, then threshold friendly. No, the non threshold friendly.
Autist Note: there is a way to compute easiness. You keep track of number of rounds of communication and complexity. Communication complexity is roughly "how the number of channel scales with increasing N?"
In the realm of blockchains, here are some examples. Cryptographers consider ECDSA (used in both bitcoin and Ethereum) a non-threshold friendly digital signature scheme. They consider Schnorr signatures (in BTC) and BLS signatures (in Ethereum) threshold friendly.
6. The Future: Evolving
What happens if Alice wants to add a new node? and what if she also wants to change the threshold?
Cryptographers are working on that. We call it evolving secret sharing in the first case. Methods do exists, especially for Shamir secret sharing.
If you like this post, please put a like below, comment, subscribe and share on X. It's not for the algorithm: I am a dopamine monkey and I do like those kind of metrics so number go up will make me very happy.

















Very interesting and well explained!
I`m starting a career change into cryptography and crypto in general as a dev.
Keep posting you're legit!